1.1 Verspannung

1.1.1 Theorie (Werkstoffkunde)
In der Technik muss man beachten, dass alle Bauteile eine möglichst hohe Lebensdauer erreichen müssen. Deswegen kommt der Werkstoffauswahl eine besondere Bedeutung zu. Werkstoffe zeigen verschiedene Verformungs-Mechanismen wie z.B. elastische Verformung, plastische Verformung, Kristallumformung usw. Im Maschinenbau muss man den Grenzbereich zwischen der elastischen und plastischen Verformung genau beachten, da nach der elastischen Verformung die Bauteile weiter funktionsfähig sind und nach einer plastischen Verformung dauerhaft verändert und somit für den ursprünglichen Einsatzzweck nicht mehr geeignet sind.

Es wird von elastischer Verformung gesprochen, wenn nach einer niedrigen Belastung die Verformung des Bauteiles bei Entlastung wieder in den Ursprungszustand zurückkehrt. Alle Belastungen müssen auf diese Weise durchgeführt werden, der elastische Bereich darf nie verlassen werden.

Bei der plastischen Verformung ist die Verformung dauerhaft und geht bei Entlastung nicht wieder zurück. Eine bleibende Verformung findet statt.

Diese zwei Verformungsarten sind von Festigkeitskenngrößen abhängig. Diese Kenngrößen zeigen die Grenzen des Werkstoffverhaltens bei Belastung.

Die elastische Verformung befindet sich bis zum Erreichen der Elastizitätsgrenze σE unterhalb der Streckgrenze Re. Dieser zulässige Wert darf nicht überschritten werden. Oberhalb der σE – Grenze treten neben der elastischen auch plastische Verformungen auf.

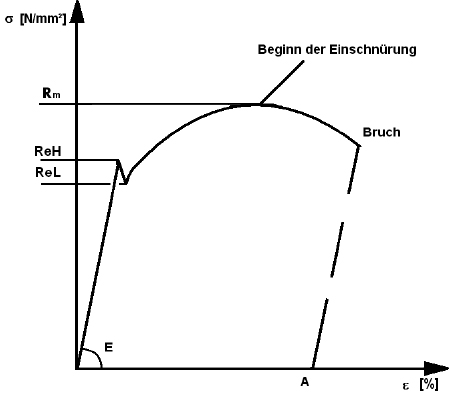
Abb. 01 Spannungs-Dehnung Diagramm

Mit zunehmender Dehnung erreicht die Spannung den Maximalwert (Zugfestigkeit) Rm. In diesem Maximum tritt eine Querschnittsverkleinerung auf (Einschnürung). Die weitere Längenänderung findet nur noch in diesem Bereich durch weitere Querschnittsveränderungen statt. Der spätere Bruch des Bauteiles wird an der Stelle mit der höchsten Einschnürung liegen. Der abnehmende Querschnitt benötigt kleinere Kräfte zu weiteren Dehnung, deshalb sinken die Kräfte und damit die Kurve bis zum Bruch.

Nach dem Hooke’schen Gesetz berechnet sich:
E: Elastizitätsmodul

ε: Dehnung mit:

Re bzw. Rp0,2: Streckgrenze mit:

Fe: Zugkraft bei der Streckgrenze

So: Querschnitt der verspannten Bauteile

Rm: Zugfestigkeit mit:

Fm: Die Höchstzugkraft
A: Bruchdehnung mit:

Lo: Anfangslänge
Lu: Bleibende Länge der Messstrecke nach dem Bruch /5/

1. Schraubenauslegung
Damit Schraubenverbindungen sicher sind, müssen die auftretenden Kräfte und Verformungen in den Schrauben und den zu verschraubenden Teilen untersucht werden.
Die Kraft-Einleitung beginnt mit dem Beidrehen der Mutter. Die zu verbindenden Teile werden gestaucht und gleichzeitig wird die Schraube gedehnt und damit vorgespannt. Die axiale Vorspannkraft liefert in der Verbindung eine Klemmkraft die wir als Fkl bezeichnen.

Nach dem Hookeschen Gesetz ist die elastische Längenänderung in der Schraube mit dem Querschnitt A:

Die elastische Nachgiebigkeit ist das Verhältnis aus Längenänderung  und Kraft F.

Die Schrauben werden in mehrere Einzelelemente aufgeteilt, abhängig vom Querschnitt Ai und der Länge li. Die Nachgiebigkeit der gesamten Schraube setzt sich aus der Addition der Nachgiebigkeiten der einzelnen Elemente zusammen:

Die spez. Nachgiebigkeit jeder einzelnen Schraube muss dabei bestimmt werden, um eine exakte Verspannung gewährleisten zu können. Hier ist schwierig festzustellen, welche Bereiche an der Verformung teilgenommen haben. Es hängt von den Durchmessern der verschraubten Teile DA und den Kopfauflagedurchmessern dw ab (siehe Abb. 3-2).

Wenn DA>dw verbreitet sich die druckbeanspruchte Zone vom Schraubenkopf zur Trennfüge hin. Verformungen in diesem Fall werden gleichmäßig verteilt. In diesen Fall ist es notwendig einen Ersatzquerschnitt zu bestimmen:

x:

dw: Außendurchmesser der ebenen Kopfauflagefläche ggf. auch Schlüsselweite.
DA: Außendurchmesser der verspannten Hülse.
dh: Durchmesser des Durchgangsloches.

Abb. 02 zylindrische Durchsteckschraubverbindung mit Verformungskegel und – Hülse /6/

Bei DA dw+lk ist die Gleichung identisch.
Bei DA=dw+lk bleibt der Ersatzquerschnitt annähernd konstant.
Bei DA dw

Die elastische Nachgiebigkeit ergibt sich nach der Gleichung:

lk: Klemmlänge der verspannten Teile
Aers: Ersatzquerschnitt
ET: Elastizitätsmodul der verspannten Teile
Fv: Vorspannkraft

Beim statischen Fall, bei der die Betriebskraft FB auf die vorgespannte Verbindung wirkt, ergibt sich eine zusätzliche Dehnung ΔfS. Eine gleiche Entspannung ΔfT wird in den zu verbindenden Teilen stattfinden (siehe Abb. 3-3)

Abb. 03 Kräfte und Verformungen an einer vorgespannten Schraubenverbindung /7/

In diesem Fall nimmt die Vorspannkraft FV ab und die Restklemmkraft in den Teilen wird:

FBT: Entlastungskraft

Die Gesamtschraubenkraft wird dann (siehe Abb. 3-4):

FB: Zusatzkraft
FBS: Zusätzlich belastender Anteil der Schraube von FB

Einen Sicherheitsabstand νA zur Streckgrenzenkraft FS bzw. F0,2 muss FSges haben, um dauerhaft Verformungen zu vermeiden und weitere Einsätze der Schraube zu ermöglichen. Der vorgespannte Zustand mit FV stellt sich wieder ein, wenn die Wirkung von FB aufhört.

Die Zusatzkraft für die Schraube lässt sich aus Ähnlichkeitsbetrachtungen am Verspannungsschaubild (siehe Abb. 3-4) und durch Einführen der elastischen Nachgiebigkeit δS und δT sowie des Kraftverhältnisses Φ ableiten.

Φ: Kraftverhältnis mit:

Abb. 04 Verspannungsschaubild /7/

Die Entlastungskraft für die Teile wird:

damit die Klemmkraft zwischen den Bauteilen:

Bei Krafteinleitung über die Schraubenkopf- und Mutterauflage gilt:

Bei Krafteinleitung über die verspannten Teile:

n: Krafteinleitungsfaktor (siehe Abb. 3-5)

Abb. 05 Krafteinleitungsfaktoren für typische Konstruktionsfälle /7/

Querbeanspruchte, reibschlüssige Schraubenverbindung
Deckelverschraubung mit weit von der Trennfuge liegendem Kraftangriffspunkt (ungünstig)
und d) mit näher zur Trennfuge rückendem Kraftangriffspunkt (günstiger)

Für jeden beliebigen Kraftangriff ergibt sich ein bestimmter Krafteinleitungsfaktor. Dieser Faktor liegt zwischen 0 und 1. Es ist besonders darauf hinzuweisen, dass eine Rechnung mit der Annahme, dass die Betriebskraft direkt unter dem Schraubenkopf angreift, für die Schraube die ungünstigsten Ergebnisse liefert. In diesem Fall nimmt der Krafteinleitungsfaktor n den Wert 1 ein. Im Idealfall, für n=0, wird die Betriebskraft direkt in der Trennfuge eingeleitet was kaum zu realisieren ist. In der Praxis setzt man den Wert n=0,5, in günstigeren Fällen n=0,3. Verschiedene Einsatzfälle sind in Abb. 3-5 gezeigt.

Den dynamischen Betriebsfall werden wir nicht betrachten, da wir nur mit statischen Belastungen arbeiten werden.

Nicht zu vernachlässigen ist das „Setzen“ von Schraubverbindungen, da es zu sehr großen Vorspannkraftverlusten der verspannten Teile führen kann. Alle im Eingriff stehenden Flächen werden aufgrund des Setzvorgangs durch Oberflächenrauheiten plastisch verformt, da wir hohe Flächenpressungen erzielen. Diese bewirken zum einen eine Verringerung der Plattendicke und zum anderen eine Reduzierung der Vorspannkraft um den Betrag FZ (siehe Abb. 3-6). Die Vorspannkraft FV muss deshalb so hoch gewählt werden, dass beim Einleiten einer Betriebskraft FB in die Schraubenverbindung die Restklemmkraft nicht gleich Null wird bzw. eine geforderte Klemm- oder Dichtkraft FKL nicht eingehalten werden kann. Ist der Verlust der Vorspannkraft FZ bei Wirken der Betriebskraft FB so groß, dass die geforderte Klemmkraft FKl=0 wird, so würden die zu verbindenden Teile lose aufeinander liegen. Es ist daher erforderlich, den Vorspannverlust FZ bei der Schraubenberechnung zu berücksichtigen.

Setzbeträge treten beispielsweise in folgenden, mit Druck belasteten Flächen auf:

• In miteinander verschraubten Gewinden von Schraubenbolzen und Mutter
• In auf Druck beanspruchten Flächen unter dem Schraubenkopf bzw. der Mutter
• In sämtlichen Trennfugen der verspannten Teile

Die Setzbeträge gelten nur für den Fall, in dem Grenzflächenpressungen nicht überschritten werden sollen, da sonst sehr viel größere Vorspannkraftverluste eintreten.

Abb. 06 Verspannungsschaubild mit Vorspannkraftverlusten /7/

Der Zusammenhang zwischen FZ und dem Setzbetrag fZ wird:

Der Vorspannkraftverlust ergibt sich unter Berücksichtigung des Kraftverhältnisses „Φ“ (siehe Gl. 2-18) aus der Formel:

Die weitgehende Einebnung der Oberflächenrauheiten während des Anziehens ist der Grund dafür, dass Setzbeträge fast unabhängig von der Rauigkeit der Fügeflächen und der Anzahl der Trennfugen sind.

Nach experimentellen Untersuchungen und für massive Verbindungen mit Schrauben nach DIN 931 hat man für den Setzbetrag festgestellt, dass:

Für Dehnschaft, Hohl- und ähnliche Schrauben in massiven Verbindungen gilt:

Bei sehr nachgiebigen Verbindungen müssen Setzbeträge durch Versuche ermittelt werden.

Ebenfalls exakt beachten muss man die Schraubenfestigkeitsklassen. Es handelt sich bekanntlich um eine Kombination von 2 Ziffern z.B. 8.8 bzw. 10.9. Alle Schrauben sind mit Festigkeitsklassen gekennzeichnet. Diese Kennzeichnung eröffnet uns sehr rasch die wichtigsten Daten der Schraube, die Zugfestigkeit Rm und die Streckgrenze Re bzw. die 0,2%-Dehngrenze Rp0,2. Als Beispiel nehmen wir die Schraube 8.8:

1. Bestimmung von Rm: Der erste Wert multipliziert mit 100 ergibt

2. Bestimmung von Re bzw. Rp0,2: Der erste Wert mit dem zweiten Wert multipliziert und das Ergebnis mit 10 multipliziert ergibt

Genaue Erklärungen zu Rm und Re siehe 3.1.1 Theorie (Werkstoffkunde). /7/
Die Herstellung von Schrauben erfolgt vorzugsweise spanlos durch Pressen, Stauchen, Eindrücken, Rollen, oder spannend durch Drehen, Fräsen und Schleifen.
Die Herstellungsart ist abhängig vom: Werkstoff, der geforderten Genauigkeit, der Gewindeform, der Stückzahl und der erforderlichen Festigkeit.

Mehrere Rechenschritte sind erforderlich, um eine Schraubenverbindung zu berechnen. Für jeden Verschraubungsfall sind besondere Rechenschritte zu beachten. In unserem Fall geht die Berechnung von der Betriebskraft FB aus, die von außen auf die Verbindung wirkt. Diese Betriebskraft liefert an den einzelnen Verschraubungsstellen eine axiale Betriebskraft FA, eine Querkraft FQ, ein Biegemoment Mb und anschließend ein Drehmoment MT.

Die Hauptdimensionierungsformel, einer Schraubenberechnung lautet:

αA: Anziehfaktor

FZ, ΔFVth: Vorspannkraftverluste

Die Fehler beim Abschätzen der Reibungszahlen, das Anziehverfahren, die Gerätetoleranzen sowie die Bedienungsfehler und Ableseungenauigkeiten sind durch den Anziehfaktor αA berücksichtigt. Man kann den Anziehfaktor auch als Verteilungskoeffizient zwischen FM min und FM max verstehen. Unter Beachtung der Anzieh- und Einstellverfahren sowie der Reibungszahlklassen ist der Anziehfaktor nach Tabelle A8 zu ermitteln.

Bei der streckgrenzgesteuerten und drehwinkelgesteuerten Anziehverfahren gilt α=1

Um den Schraubennenndurchmesser zu bestimmen muss die Montagevorspannkraft FM bekannt sein. Eine zugeordnete Spannkraft FM, die mindestens so groß wie die rechnerische Montagevorspannkraft FM max unter Berücksichtigung der Festigkeitsklasse und der Reibungsverhältnisse ist, darf die gewählte Schraube nicht überlasten. Eine Schraube wird in der Regel mit 90% ihrer Mindeststreckgrenze ausgelegt. Eine Überprüfung der Flächenpressung wird in der Berechnung ebenfalls berücksichtigt.

Die Rechenschritte werden wie folgt durchgeführt:

• Ermittlung des Nenndurchmessers d und der zugehörigen Festigkeitsklasse

Wegen der Art der Verbindungen und der Betriebskraft ist der Nenndurchmesser aus Anhang Tabelle A7 zu ermitteln. Die zugehörige Festigkeitsklasse muss auch beachtet werden, da in verschiedenen Festigkeitsklassen verschiedene Nenndurchmessergrößen gewählt werden können.

• Ermittlung der Flächenpressung an den Auflageflächen

Die Grenzflächenpressung darf nicht überschritten werden, um Setzerscheinungen und dadurch plastische Verformungen der Auflageflächen zu vermeiden. Mit der maximalen Schraubenkraft Fs max gilt für die Flächenpressung unter der ebenen Kopf – bzw. Mutterauflage:

AP: Fläche der Schraubenkopf – bzw. Mutterauflage, 
PG: Grenzflächenpressung
FSP: Spannkraft für Dehnschraube bei dT < ds

dT: Schaftdurchmesser bei Dehnschrauben, dT= 0,9 x d3
dS: Durchmesser zum Spannungsquerschnitt AS, dS=(d2+d3) / 2
d2, d3: Flanken – bzw. Kerndurchmesser des Gewindes
σM: Montagezugspannung infolge FSP

dS: Durchmesser zum Spannungsquerschnitt AS, dS=(d2+d3) / 2
d2, d3: Flanken – bzw. Kerndurchmesser des Gewindes
σM: Montagezugspannung infolge FSP

Handelt es sich um ein p > pG, müssen die Konstruktionsbedingungen geändert werden.

• Ermittlung der erforderlichen Montagevorspannkraft FM

Die Montagevorspannkraft wird durch die Reibungsverhältnisse zwischen Gewinde und Auflage, geometrische Form und Festigkeit der Verbindung, das Anziehverfahren und dem Anziehgerät der Schraubenverbindungen beeinflusst.

Die Montagevorspannkraft ergibt sich aus der Formel

Die Montagevorspannkraft muss kleiner oder gleich FSP sein. Wenn dies nicht der Fall ist, muss der Schraubendurchmesser oder die Festigkeitsklasse korrigiert werden. Die Montagevorspannkraft für verschiedene Schraubengrößen mit Berücksichtigung der Festigkeitsklassen und Reibungszahlen befinden sich in Anhang Tabelle A1 – A4.

• Ermittlung des erforderlichen Anziehdrehmoments MADas Anziehdrehmoment ist der Zusammenhang zwischen dem Gewindemoment und dem Kopf- bzw. Mutterreibungsmoment. Die Reibungszahlen μG und μK sind Anhang Tabelle A5 zu entnehmen.

  P: Gewindesteigung
  d2: Flankendurchmesser
  DKm: Reibungsdurchmesser unter dem Kopf

  mit

  Da: Fasendurchmesser der Mutter
  dha: Fasendurchmesser an den verspannten Teilen
  dh: Bohrungsdurchmesser
  da: Innendurchmesser der ebenen Kopfauflage

  Die Anziehdrehmomente MA für verschiedene Schraubengrößen mit Berücksichtigung der Festigkeitsklassen und Reibungszahlen befinden sich in Anhang Tabelle A1 – A4. Eine Nachprüfung bei statischer Betriebskraft ist normalerweise nicht erforderlich. In unsicheren Fällen oder wenn FSP nicht bekannt ist, muss man die Vergleichsspannung σred nachprüfen.

  

  mit

  σM: siehe Gleichung 3-29

  Wp: polares Widerstandsmoment mit

  Eine Nachprüfung der Flächenpressung unter Kopf- bzw. Mutterauflage ist mit Gleichung 3-26 durchzuführen. /7/